iniziamo una discussione sul money management "masaniello" originato dal mondo delle scommesse e possibilità di implementazione nel trading.
Origine e scopo di fondo dell’utilizzo del money management “masaniello”
http://www.skillandbet.com/sistema-d...asaniello.html
È uno dei sistemi più conosciuti nella comunità di scommettitori italiani. Nato nel 2002, anno in cui Massimo Mondò ebbe l’intuizione e Ciro Masaniello ne realizzò l’algoritmo di calcolo, tale strumento è stato perfezionato nel corso degli anni ed ha raggiunto ora un certo grado di
complessità.
Lo scopo del metodo, come riportato dagli autori, è quello di ottenere rendimenti superiori rispetto alle giocate tradizionali "a combinazione" a parità di eventi indovinati.
Vediamo un esempio:
se provassimo 10 scommesse/operazioni a quota 2, con una cassa = 100, giocando, con una impostazione tradizionale, per ogni evento una posta = cassa/n = 10,
ed indovinando k=5 eventi su n=10 totali, otterremmo un guadagno netto pari a zero, perché su 5 eventi guadagneremmo 50 e sugli altri 5 eventi perderemmo 50.
Invece, le stesse operazioni inserite in un money management “Masaniello” ci darebbero una probabilità pari al 62.305% di ottenere su n=10 prove ALMENO k=5 vittorie, da cui risulta un guadagno netto pari a (cassa*0.605) cioè il 60.5% della cassa.
Naturalmente tale maggior rendimento ha un prezzo da pagare, che consiste nella perdita totale della cassa se non vengono indovinate almeno k=5 eventi su n=10.
Infatti, se il giocatore indovina solo 4 delle 10 operazioni, perde comunque l’intera cassa iniziale di 100,
mentre nell'impostazone tradizionale una parte della cassa si sarebbe salvata, perché su k=4 eventi guadagnerebbe 40 e sui rimanenti 6 eventi sbagliati perderebbe 60, da cui una perdita di soli 20.
Di seguito due domande e risposte molto utili per formarci una base comune su cui poi poter eventualmente discutere.
°°°°°°°°°°°°°°°°°°°°°°°°°°
Perché la quota per scommesse si calcola sempre con la formula: 1 / probabilità di un esito di scommessa ?
La "quota" è il valore a cui moltiplicare la puntata dello scommettitore per calcolare il compenso se l'evento va come ipotizzato dallo scommettitore.
Nel mondo delle scommesse, gli operatori o bookmakers che propongono una scommessa per un evento valutano a priori la probabilità degli esiti dell'evento.
Ad esempio, se nella partita Milan-Roma gli operatori ritengono la squadra del Milan favorita, grazie al vantaggio casalingo ed alla buona forma attuale, valutano la probabilità di una vittoria del Milan al 50%, quella di un pareggio al 30% e quella di una vittoria della Roma al 20%.
Perciò, secondo i bookmakers, un giocatore che vuole scommettere 10 euro sull'esito della partita Milan-Roma, se punta questi soldi
- sulla vittoria del Milan, ha una probabilità del 50% di vincere e 50% di perdere, cioè il rapporto tra probabilità di vincere e probabilità di perdere è di 50:50 --> 1:1
- sul pareggio, ha una probabilità del 30% di vincere e 70% di perdere, cioè il rapporto tra probabilità di vincere e probabilità di perdere è di 30:70 --> 1:70/30 --> 1:2.33
- sulla vittoria della Roma, ha una probabilità del 20% di vincere e 80% di perdere, cioè il rapporto tra probabilità di vincere e probabilità di perdere è di 20:80 --> 1:80/20 --> 1:4
Se in un gioco si ha una probabilità p che accada un evento E che permette di vincere una somma S, si definisce speranza matematica della somma S il prodotto della somma S per la probabilità p che accada l’evento E: SperanzaMatematica = S * p(E)
Per un giocatore la speranza matematica dell'evento partita Milan-Roma, a fronte di una posta A della scommessa, è di guadagnare
- una somma S1 per la vittoria del Milan, che ha probabilità p(E)=50%,
- o una somma S2 per il pareggio, che ha probabilità p(E)=30%,
- o una somma S3 per la vittoria della Roma, che ha probabilità p(E)=20%.
Quanto devono valere queste somme S1, S2 e S3? Qui entra in campo la definizione di "gioco equo".
Un gioco si dice "equo" quando il guadagno medio prevedibile o speranza matematica o valore atteso è nullo per ciascun giocatore, cioè quando probabilisticamente nessun giocatore risulta avvantaggiato nel lungo periodo rispetto all’altro, cioè alla fine i giocatori antagonisti si trovano a non aver né guadagnato né perso.
Il giocatore sta scommettendo in un gioco equo se la posta A che è disposto a pagare per parteciparvi è uguale alla speranza matematica, cioè al prodotto della vincita S per la probabilità p di ottenerla.
S * p(E) = A
da cui si ricava il guadagno "giusto" del giocatore se indovina la scommessa: S = A / P(E)
che si può scrivere anche come S = A * quota con quota = 1/p(E)
Quindi una scommessa risulta "equa" se la vincita S che possiamo realizzare è uguale a 1/p volte la posta A che abbiamo pagato per parteciparvi.
La quota per le scommesse si calcola sempre con questa formula: 1 / probabilità di un esito di scommessa,
perché consideriamo la scommessa come un gioco equo, anche se in realtà il gioco non è equo ma sempre un po' a favore del bookmaker.
Nell'esempio dell'evento partita Milan-Roma le quote proposte dal bookmaker per le tre scommesse saranno quindi:
vincita Milan : p=50% --> quota = 1/0.5 = 2,00 --> S = A * quota
pareggio : p=30% --> quota = 1/0.3 = 3,33 --> S = A * quota
vincita Roma : p=20% --> quota = 1/0.2 = 5,00 --> S = A * quota
In realtà il gioco equo con le scommesse sportive non esiste, perché naturalmente il bookmaker deve guadagnare dal suo lavoro.
Ed infatti... ogni società che gestisce le scommesse ha la certezza statistica di vincere denaro, perché le quote che offre sono sempre inferiori a quanto il gioco equo richiederebbe, cioè sono inferiori all’inverso della probabilità di vittoria.
Una scommessa è conveniente al giocatore quando la quota pagata è maggiore dell’inverso della probabilità di vittoria.
Immaginate di giocare a testa o croce e di scommettere su testa; la probabilità di vittoria è del 50%, e quindi la quota per cui il gioco non è ne vincente ne perdente è di 2.
Se il bookmaker pagasse 2,1 allora la scommessa sarebbe statisticamente vincente, altrimenti statisticamente perdente: questo significa che sebbene non si possa affermare che sulla singola scommessa guadagnerò del denaro o meno, posso ragionevolmente confidare che su tante giocate le scommesse statisticamente vincenti mi faranno guadagnare.
Ovviamente tutti i bookmaker propongono soltanto scommesse statisticamente perdenti, il che conferisce loro, su molte giocate, una statistica certezza di guadagno.
Provando ad andare su un qualunque sito di scommesse, si osserva come per tutte le scommesse la somma degli inversi delle quote è un numero maggiore di 1, il che significa che per i giocatori le scommesse sono statisticamente perdenti.
Un esempio: per una partita di calcio si leggono le seguenti quote:
1: 2.1
X: 3.1
2: 3.4
e la somma degli inversi 1/2.1 + 1/3.1 + 1/3.4 = 1,093 : questo comporta che statisticamente, per la partita in esame il bookmaker guadagna il 9,3%
°°°°°°°°°°°°°°°°°°°°°°°°°°
Perché la quota per una scommessa espressa con un rapporto rendimento/rischio del tipo 1:x
si calcola con la formula 1 + x ?
Riprendendo la formula quota = 1/p(E)
per una variabile binomiale con n=1 , dove i risultati possibili di ciascuna prova possono essere soltanto due:
- successo (p=probabilità favorevole all'evento)
- insuccesso (q=1-p = probabilità sfavorevole all'evento)
con p + q = 1
si ha:
quota = 1/p
Se il rapporto rendimento/rischio è espresso come 1 : x
si ha:
quota = 1 + x = 1 + q/p
Infatti, essendo per definizione p + q = 1
quota = 1/p = (p + q)/p --> quota = 1 + q/p
Ad esempio, nella partita di calcio Milan-Roma,
quando il broker offre la singola scommessa (n=1) del pareggio a 1 : 2.33,
sta affermando che ritiene la probabilità che la Roma pareggi sia del 30%.
Facendo i calcoli…
p=0.3 probabilità di successo dell’evento pareggio
q=0.7 probabilità di insuccesso dell’evento pareggio
p + q = 0.3 + 0.7 = 1
quota = 1/p = 1/0.33 = 3.33
ed infatti q/p = 0.3/0.7 = 2.33
come offerto dal broker 1:2.33 = 1:q/p
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
Origine e scopo di fondo dell’utilizzo del money management “masaniello”
http://www.skillandbet.com/sistema-d...asaniello.html
È uno dei sistemi più conosciuti nella comunità di scommettitori italiani. Nato nel 2002, anno in cui Massimo Mondò ebbe l’intuizione e Ciro Masaniello ne realizzò l’algoritmo di calcolo, tale strumento è stato perfezionato nel corso degli anni ed ha raggiunto ora un certo grado di
complessità.
Lo scopo del metodo, come riportato dagli autori, è quello di ottenere rendimenti superiori rispetto alle giocate tradizionali "a combinazione" a parità di eventi indovinati.
Vediamo un esempio:
se provassimo 10 scommesse/operazioni a quota 2, con una cassa = 100, giocando, con una impostazione tradizionale, per ogni evento una posta = cassa/n = 10,
ed indovinando k=5 eventi su n=10 totali, otterremmo un guadagno netto pari a zero, perché su 5 eventi guadagneremmo 50 e sugli altri 5 eventi perderemmo 50.
Invece, le stesse operazioni inserite in un money management “Masaniello” ci darebbero una probabilità pari al 62.305% di ottenere su n=10 prove ALMENO k=5 vittorie, da cui risulta un guadagno netto pari a (cassa*0.605) cioè il 60.5% della cassa.
Naturalmente tale maggior rendimento ha un prezzo da pagare, che consiste nella perdita totale della cassa se non vengono indovinate almeno k=5 eventi su n=10.
Infatti, se il giocatore indovina solo 4 delle 10 operazioni, perde comunque l’intera cassa iniziale di 100,
mentre nell'impostazone tradizionale una parte della cassa si sarebbe salvata, perché su k=4 eventi guadagnerebbe 40 e sui rimanenti 6 eventi sbagliati perderebbe 60, da cui una perdita di soli 20.
Di seguito due domande e risposte molto utili per formarci una base comune su cui poi poter eventualmente discutere.
°°°°°°°°°°°°°°°°°°°°°°°°°°
Perché la quota per scommesse si calcola sempre con la formula: 1 / probabilità di un esito di scommessa ?
La "quota" è il valore a cui moltiplicare la puntata dello scommettitore per calcolare il compenso se l'evento va come ipotizzato dallo scommettitore.
Nel mondo delle scommesse, gli operatori o bookmakers che propongono una scommessa per un evento valutano a priori la probabilità degli esiti dell'evento.
Ad esempio, se nella partita Milan-Roma gli operatori ritengono la squadra del Milan favorita, grazie al vantaggio casalingo ed alla buona forma attuale, valutano la probabilità di una vittoria del Milan al 50%, quella di un pareggio al 30% e quella di una vittoria della Roma al 20%.
Perciò, secondo i bookmakers, un giocatore che vuole scommettere 10 euro sull'esito della partita Milan-Roma, se punta questi soldi
- sulla vittoria del Milan, ha una probabilità del 50% di vincere e 50% di perdere, cioè il rapporto tra probabilità di vincere e probabilità di perdere è di 50:50 --> 1:1
- sul pareggio, ha una probabilità del 30% di vincere e 70% di perdere, cioè il rapporto tra probabilità di vincere e probabilità di perdere è di 30:70 --> 1:70/30 --> 1:2.33
- sulla vittoria della Roma, ha una probabilità del 20% di vincere e 80% di perdere, cioè il rapporto tra probabilità di vincere e probabilità di perdere è di 20:80 --> 1:80/20 --> 1:4
Se in un gioco si ha una probabilità p che accada un evento E che permette di vincere una somma S, si definisce speranza matematica della somma S il prodotto della somma S per la probabilità p che accada l’evento E: SperanzaMatematica = S * p(E)
Per un giocatore la speranza matematica dell'evento partita Milan-Roma, a fronte di una posta A della scommessa, è di guadagnare
- una somma S1 per la vittoria del Milan, che ha probabilità p(E)=50%,
- o una somma S2 per il pareggio, che ha probabilità p(E)=30%,
- o una somma S3 per la vittoria della Roma, che ha probabilità p(E)=20%.
Quanto devono valere queste somme S1, S2 e S3? Qui entra in campo la definizione di "gioco equo".
Un gioco si dice "equo" quando il guadagno medio prevedibile o speranza matematica o valore atteso è nullo per ciascun giocatore, cioè quando probabilisticamente nessun giocatore risulta avvantaggiato nel lungo periodo rispetto all’altro, cioè alla fine i giocatori antagonisti si trovano a non aver né guadagnato né perso.
Il giocatore sta scommettendo in un gioco equo se la posta A che è disposto a pagare per parteciparvi è uguale alla speranza matematica, cioè al prodotto della vincita S per la probabilità p di ottenerla.
S * p(E) = A
da cui si ricava il guadagno "giusto" del giocatore se indovina la scommessa: S = A / P(E)
che si può scrivere anche come S = A * quota con quota = 1/p(E)
Quindi una scommessa risulta "equa" se la vincita S che possiamo realizzare è uguale a 1/p volte la posta A che abbiamo pagato per parteciparvi.
La quota per le scommesse si calcola sempre con questa formula: 1 / probabilità di un esito di scommessa,
perché consideriamo la scommessa come un gioco equo, anche se in realtà il gioco non è equo ma sempre un po' a favore del bookmaker.
Nell'esempio dell'evento partita Milan-Roma le quote proposte dal bookmaker per le tre scommesse saranno quindi:
vincita Milan : p=50% --> quota = 1/0.5 = 2,00 --> S = A * quota
pareggio : p=30% --> quota = 1/0.3 = 3,33 --> S = A * quota
vincita Roma : p=20% --> quota = 1/0.2 = 5,00 --> S = A * quota
In realtà il gioco equo con le scommesse sportive non esiste, perché naturalmente il bookmaker deve guadagnare dal suo lavoro.
Ed infatti... ogni società che gestisce le scommesse ha la certezza statistica di vincere denaro, perché le quote che offre sono sempre inferiori a quanto il gioco equo richiederebbe, cioè sono inferiori all’inverso della probabilità di vittoria.
Una scommessa è conveniente al giocatore quando la quota pagata è maggiore dell’inverso della probabilità di vittoria.
Immaginate di giocare a testa o croce e di scommettere su testa; la probabilità di vittoria è del 50%, e quindi la quota per cui il gioco non è ne vincente ne perdente è di 2.
Se il bookmaker pagasse 2,1 allora la scommessa sarebbe statisticamente vincente, altrimenti statisticamente perdente: questo significa che sebbene non si possa affermare che sulla singola scommessa guadagnerò del denaro o meno, posso ragionevolmente confidare che su tante giocate le scommesse statisticamente vincenti mi faranno guadagnare.
Ovviamente tutti i bookmaker propongono soltanto scommesse statisticamente perdenti, il che conferisce loro, su molte giocate, una statistica certezza di guadagno.
Provando ad andare su un qualunque sito di scommesse, si osserva come per tutte le scommesse la somma degli inversi delle quote è un numero maggiore di 1, il che significa che per i giocatori le scommesse sono statisticamente perdenti.
Un esempio: per una partita di calcio si leggono le seguenti quote:
1: 2.1
X: 3.1
2: 3.4
e la somma degli inversi 1/2.1 + 1/3.1 + 1/3.4 = 1,093 : questo comporta che statisticamente, per la partita in esame il bookmaker guadagna il 9,3%
°°°°°°°°°°°°°°°°°°°°°°°°°°
Perché la quota per una scommessa espressa con un rapporto rendimento/rischio del tipo 1:x
si calcola con la formula 1 + x ?
Riprendendo la formula quota = 1/p(E)
per una variabile binomiale con n=1 , dove i risultati possibili di ciascuna prova possono essere soltanto due:
- successo (p=probabilità favorevole all'evento)
- insuccesso (q=1-p = probabilità sfavorevole all'evento)
con p + q = 1
si ha:
quota = 1/p
Se il rapporto rendimento/rischio è espresso come 1 : x
si ha:
quota = 1 + x = 1 + q/p
Infatti, essendo per definizione p + q = 1
quota = 1/p = (p + q)/p --> quota = 1 + q/p
Ad esempio, nella partita di calcio Milan-Roma,
quando il broker offre la singola scommessa (n=1) del pareggio a 1 : 2.33,
sta affermando che ritiene la probabilità che la Roma pareggi sia del 30%.
Facendo i calcoli…
p=0.3 probabilità di successo dell’evento pareggio
q=0.7 probabilità di insuccesso dell’evento pareggio
p + q = 0.3 + 0.7 = 1
quota = 1/p = 1/0.33 = 3.33
ed infatti q/p = 0.3/0.7 = 2.33
come offerto dal broker 1:2.33 = 1:q/p
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°

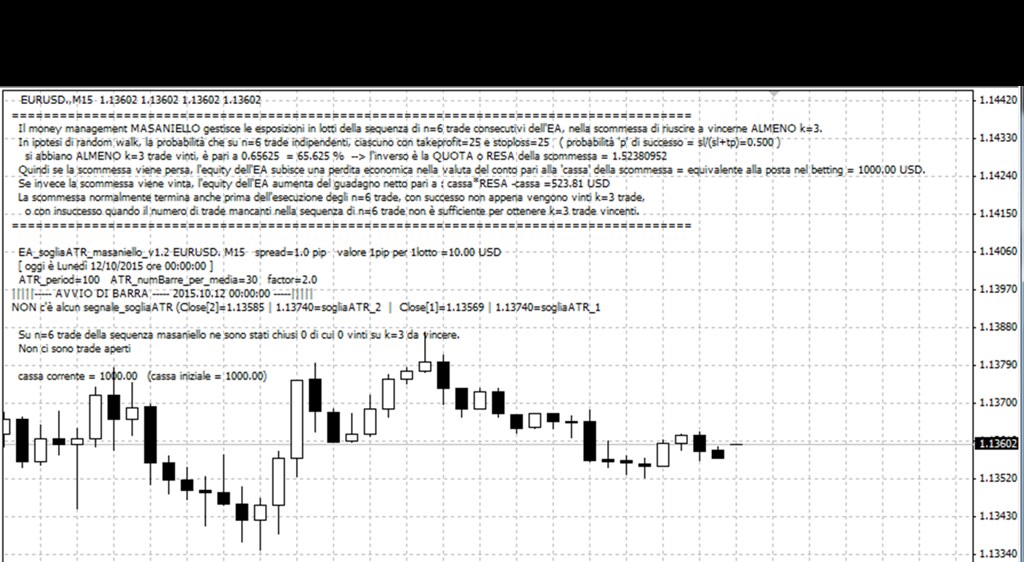
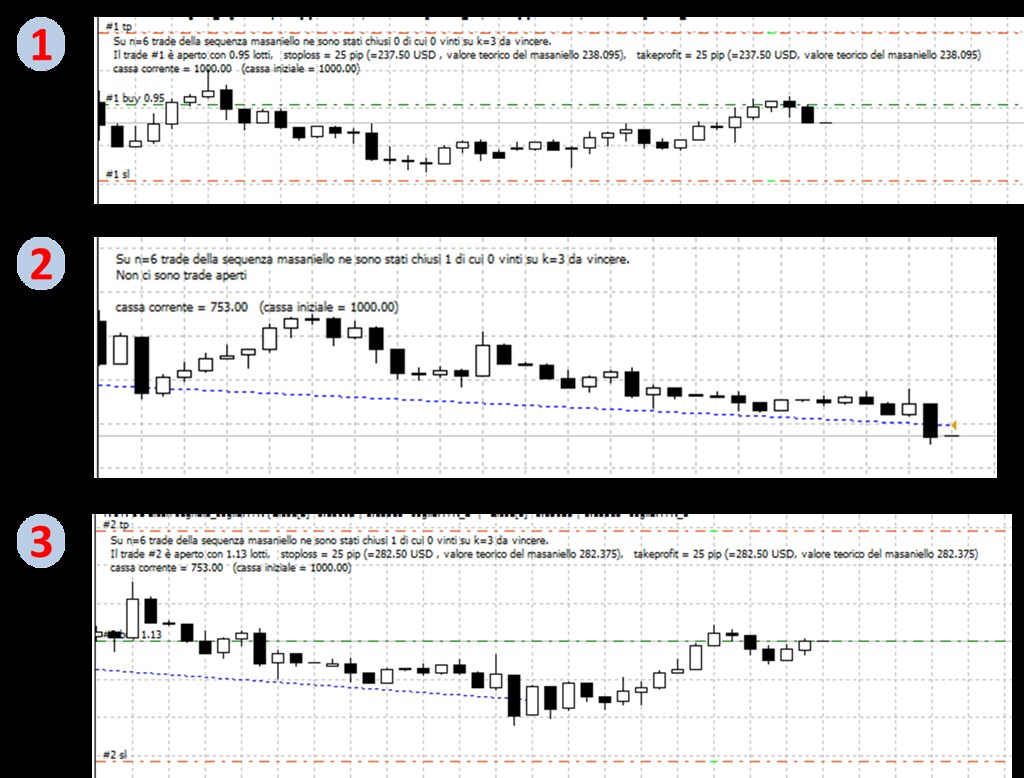
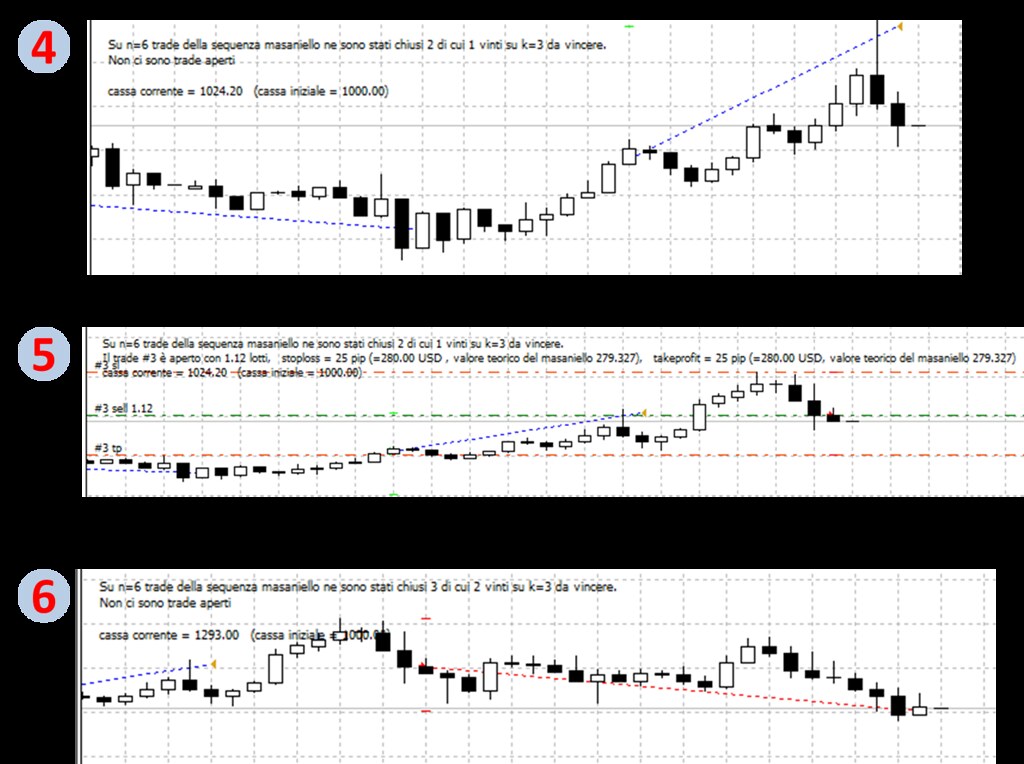
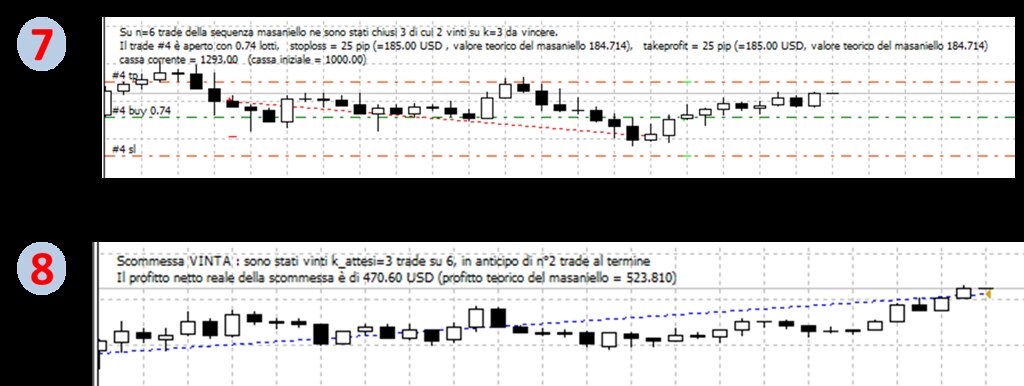



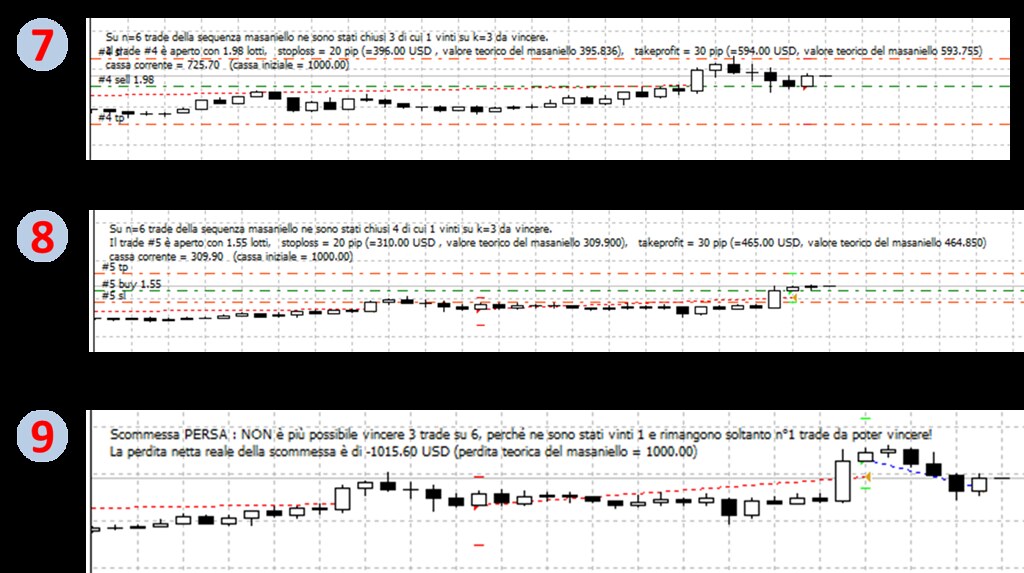

Comment